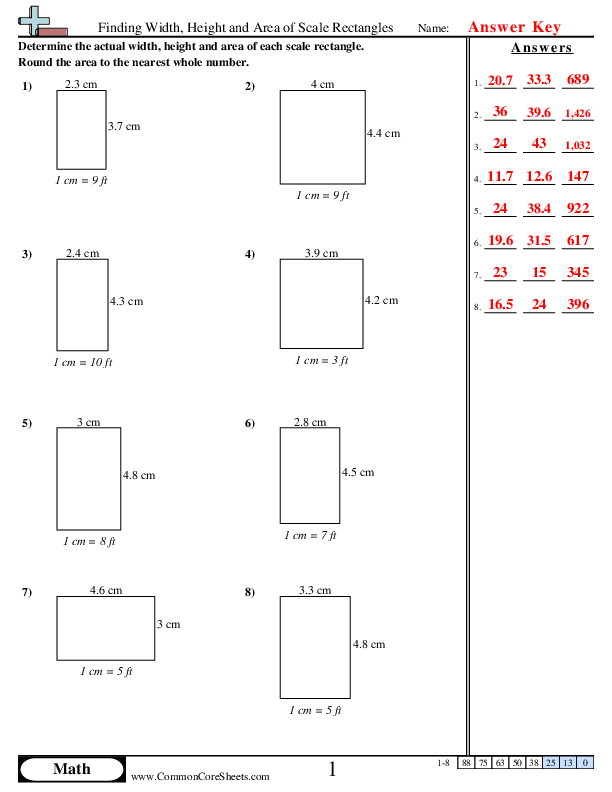
Finding Width, Height and Area of Scale Rectangles
7g1


×
Description:
"This worksheet is designed for young math enthusiasts to learn about width, height, and area of scale rectangles. With 8 customizable problems, it visualizes dimension in real-life scenarios through scaled rectangular figures, measuring in centimeters and converting to feet. The lessons can be transformed into engaging flashcards or utilized in distance learning settings, making it perfect for flexible, hands-on mathematical understanding and practice."

×
Student Goals:
Understanding of Mathematical ConceptsAfter going through the worksheet, students should have a profound understanding of the mathematical concepts associated with area, width, and height. They will comprehend the essence of these terms, as well as how they relate to the physical properties of shapes in our everyday lives.Problem-Solving Skills DevelopmentAchieving all tasks successfully in the worksheet means that a child has honed their problem-solving skills. Solving problems related to finding the dimensions and area of rectangles develops their ability to apply classroom learning to solve practical problems. Critical thinking and logical reasoning skills are also improved, making them better equipped to take on complex mathematical problems in the future.Awareness of Scale ConversionsThrough this worksheet, students will gain a basic understanding of units of measurement and how scales work in real-life scenarios. They cultivate an understanding of the concept of converting measurements from one scale to another, i.e., from centimeters to feet in this case. Learning this skill is crucial for real-life applications in construction, mapping, and other practical fields.Proficiency in Arithmetic CalculationsAfter completing the worksheet, a student should be proficient in performing basic arithmetic calculations like multiplication and division, key components in finding dimensions and areas of shapes. This solidifies their foundational knowledge in mathematics which paves the way for confidently tackling complex computations in the higher levels of education.Learning Through PracticeBy attempting different problems which follow a similar format, the student acquires the practical knowledge of the subject matter. As they say, practice makes perfect, hence the repetition of a certain type of problem ensures that the knowledge is embedded deeply into their understanding, hence becoming second nature to them.Mathematical Communication ImprovementThe written word is not just confined to languages. Math also has its own language. Students learn how to clearly express mathematical thinking by writing down the steps they follow in solving each problem, improving their mathematical literacy and communication.