3md7b Worksheets
Measurement and Data
Geometric measurement: understand concepts of area and relate area to multiplication and to addition.
7Relate area to the operations of multiplication and addition.
bMultiply side lengths to find areas of rectangles with whole-number side lengths in the context of solving real world and mathematical problems, and represent whole-number products as rectangular areas in mathematical reasoning.
3md7b
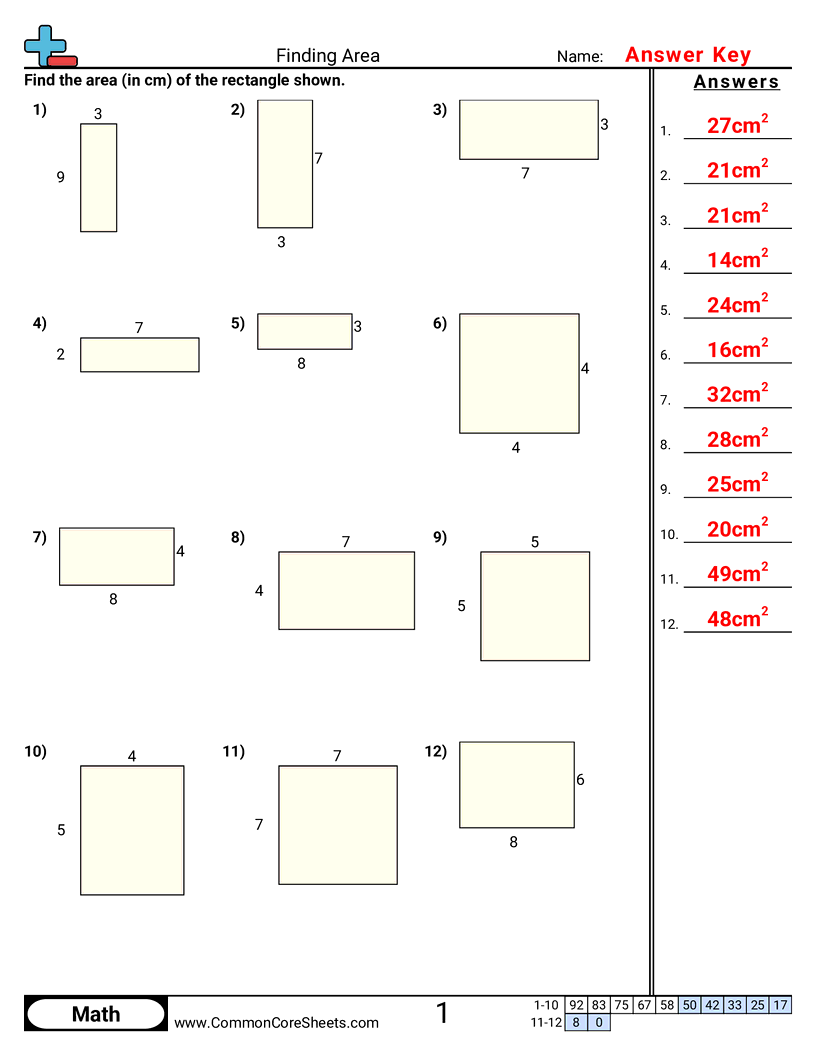
3md7b
- Find the area of a rectangle by multiplying its length and width.
- Use the correct square units (like cm² or m²) when writing an area answer.
