Identifying Rate of Change Between Two Sets
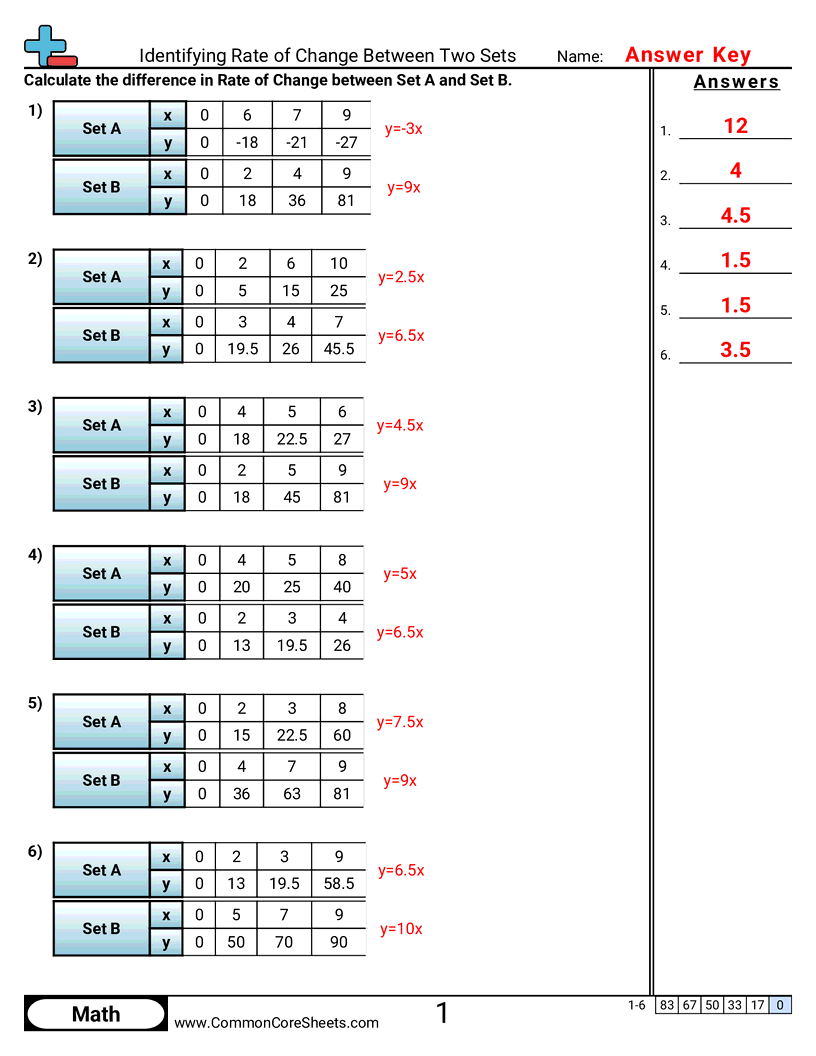
Each worksheet has 6 problems comparing the difference in rate of change between two sets.
Student Objectives
- Practice finding the rate of change (slope) for two different proportional relationships given as tables
- Calculate the difference between the two rates of change
- Work with rates that include decimals and negative numbers
Tags
Standards